La segunda práctica tambien se desarrollará en Python, en el entorno jderobot, con el simulador Gazebo.
Nuestro robot simulado, contará con 2 cámaras virtuales . Estas dos cámaras están situadas en el frontal del robot, obtienen 2 imagenes muy similares pero no exactamente iguales ya que la posición de cada cámara es distinta.
Con estas dos imágenes de la misma escena capturada por cada cámara debemos crear una imagen 3d.
Nuestro programa debe ser capaz de recrear la imagen 3d incluso para un sistema de camaras no canónico. Es decir que las dos cámaras no se encuentren en la misma altura y orientación.
El algoritmo básico comenzará tomando como referencia la imagen izquierda, recorreremos cada punto de esta imagen e intentaremos encontrar su punto homólogo en la parte derecha.
Pero la busqueda de este homólogo puede ser muy costosa, y en vez de buscarlo por toda la imagen lo buscaremos en aquellas zonas en las que sólo puede estar el punto hómologo. Es decir el homólogo en la parte derecha se encontrará en la linea epipolar.
Como conseguimos locliazar la línea epipolar en la imagen derecha? Podríamos decir que para un rayo que parte de la cámara izquierda y pasa por el punto X,Y de la imagen izquierda, la proyección de dicho rayo en la imagen derecha sería la línea epipolar. Por tanto sólo tendríamos que buscar el homologo de un punto de la imagen izquierda en una estrecha franja de la imagen derecha.
Para conseguir la linea epipolar, necesitaremos 2 puntos 3D de la imagen izquierda. El primero será la retroproyección del punto 2D que pasa por las coordenadas XY de la imagen izquierda y que llamaremos P1. El segundo punto 3D , P2, será un punto muy alejado de P1 pero que esté en el mismo rayo que P1, es decir que el rayo de retroproyección de P1 también pase por P2.
Encontrar un tercer punto en una linea 3D
Tras conseguir los dos puntos 3D P1 y P2 en la imagen izquierda, los proyectaremos en la imagen derecha. Tras esta proyección obtendremos 2 puntos 2D de la imagen derecha, calcularemos la pendiente de la recta 2D que pasa por estos 2 puntos y así podremos calcular la recta que une estos 2 puntos 2D en la imagen derecha , esta recta es la línea eipolar.
La búsqueda del punto homólogo en la imagen derecha se reducirá solo a la franja eipolar. La franja eipolar se obtiene tomando cada pixel de la línea epipolar y añadiendo por ejemplo 5 pixeles superiores y otros 5 pixeles inferiores a la coordenada Y de cada punto. La busqueda se realizará localizando pequeños parches de la imagen izquierda en una pequeña zona de la linea epipolar, normalmente utilizaremos parches de 11×11
Para la busqueda del homólogo con openCV , utiliaremos correlación y la función macheo utilizaremos
cv2.matchTemplate(self.edgesRight[y-11:y+11,x-11:x+11],template,cv2.TM_CCORR_NORMED)
min_val, max_val, min_loc, max_loc = cv2.minMaxLoc(res)
http://docs.opencv.org/3.1.0/d4/dc6/tutorial_py_template_matching.html#gsc.tab=0
Una vez encontrado el homólogo en la imagen derecha , trataremos de calcular las coordenadas del punto3D donde se cruzan los rayos de retroproyección provenientes del punto 3d de la imagen izquierda y del homólogo en la imagen derecha . Probablemente estos 2 rayos no lleguen a cruzarse y tendremos que encontrar el segmento más corto entre ellos. Una vez encontrado el segmento, calcularemos el punto medio y esa será nuestra estimación del punto de corte de los 2 rayos.
Para calcular el segmento más corto entre 2 rayos se ha traducido el siguiente código de C a Python.
Calcular el segmento mas corto entre 2 rectas 3d
Resumiendo , los pasos a realizar serían:
-Leer las 2 imágenes RGB
-Transformarlas a blanco y negro
-Obtener los bordes de la imagen izquierda y derecha aplicando canny. Solo calcularé la profundidad de los puntos que sean borde
-Para cada punto P1 de los bordes, calculare su rayo de retroproyección, y un segundo punto P2 por el que pase ese mismo rayo pero mucho más alejado de la cámara y de P1.
-Estos dos puntos P1 y P2 los proyectaré en la iamagen derecha, calculare la pendiente de la recta que pasa por los 2 puntos y así obtendré la línea epipolar.
-Despues, se aplicarán convoluciones sobre línea epipolar para encontrar en la imagen derecha P1′ , el homólogo a P1.
-Una vez encontrado el homólogo, mediante triangulación calcularé el segmento más corto que pasa por la retroproyeccción de los rayos que pasan por P1 y P1′ , si esta ditancia es más corta que un umbral se obtendrá el punto medio del segmento como coordenada Z y se pintará el punto en 3D
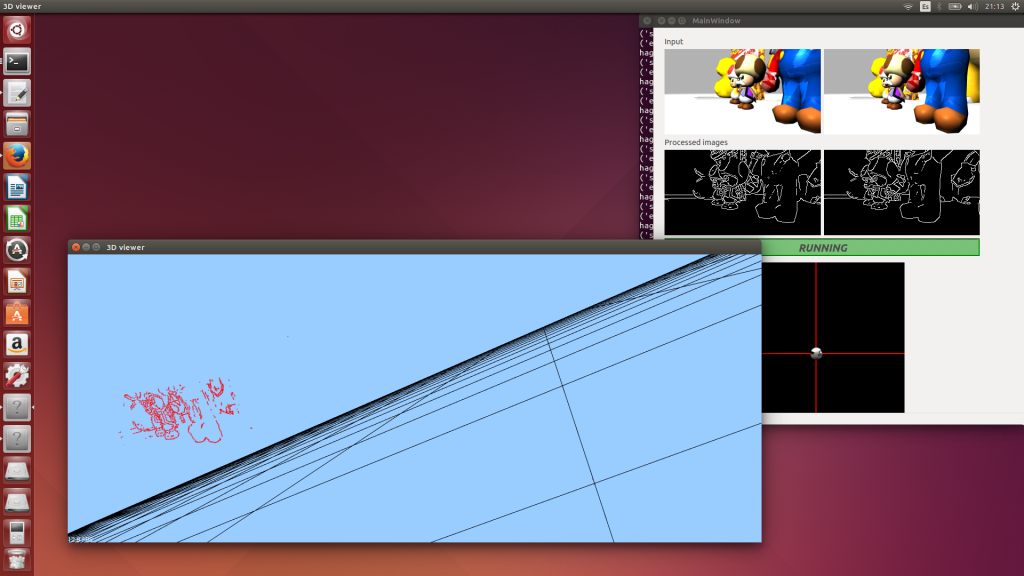
En las siguientes pantallas indicaremos como hemos ido calculando los resultados
Tras calcular la línea epipolar, tendremos que calcular el matching en la imagen derecha.
Aquí la primera imagen del matching
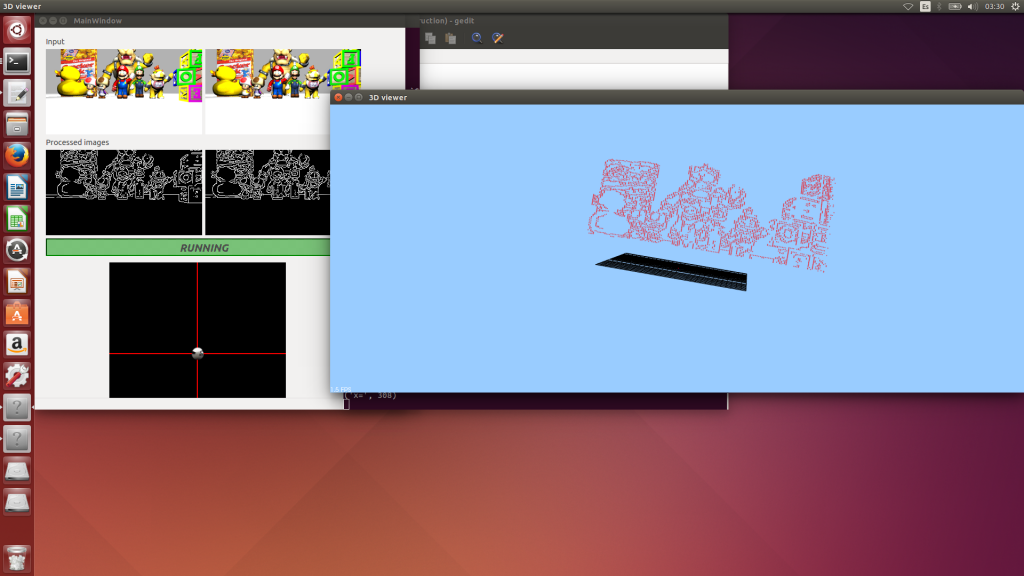
Despues conseguimos la siguiente imagen , donde aparece un matcheo de toda la imagen derecha
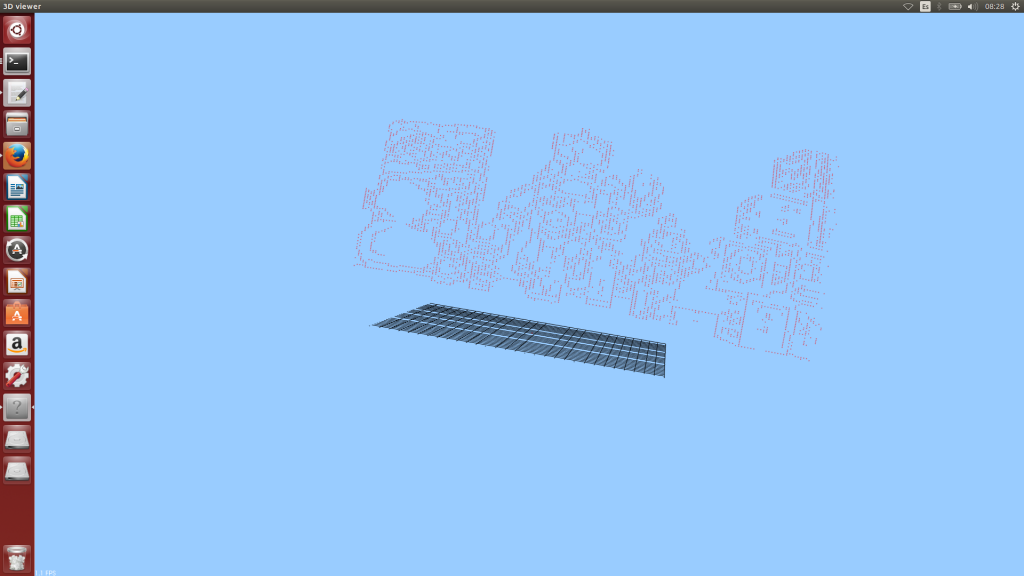
Por ultimo solo queda hayar el punto de corte, entre el rayo emitido desde la cámara izquierda y que pasa por el pixel de la imagen izquierda x,y , con el rayo que parte de la camara derecha y pasa por el pixel x,y de la imagen derecha que ha sido elegido por el macheo en la linea epipolar.